An Emergency Help Document for Those Horrified, Disgusted or Otherwise Afflicted by Infinities in QFT

On mobile devices, read the page in horizontal/"landscape" mode. Otherwise math may not fit the screen.

You’re listening to a lecture on quantum field theory. Finally, the equations of motion have been derived, the fields quantized and the reduction formulae derived. It is finally time to solve a real QFT problem – to do a perturbation theory calculation!

All of a sudden – unprompted and unwanted – the calculation leads to a divergent integral. WHAT?? How can a physical quantity be infinite?

Before you descend in to a frenzy, the lecturer provides much-needed assurance. There’s no problem, he explains – all we have to do is to regularize and renormalize! Just pretend the integral is finite after all by imposing some cutoff $\Lambda$ ("regularize"), and add some terms to your theory that remove the terms that go to infinity as the cutoff $\Lambda$ is removed ("renormalize").

You’re horrified, of course. What do you mean, $renormalize?$ How can you just go ahead and pretend the integral is finite, then erase the terms you didn’t like? Curse this quantum field theory; it’s all nonsense anyway; there’s no way this can be rigorous; I should’ve studied art history..

I’m here to tell you that the situation with infinities isn’t as bad as all that – it’s much worse. I’m also here to tell you that this is no reason to switch to art history. What sort of a coward fears a few measly infinities?

Infinities everywhere

Instead of dealing with a difficult theory like QFT, let’s deal with something our tiny brains are more in tune with: polynomials and their roots.

That’s right, it’s back to school. Polynomials! You can do them using perturbation theory, too.

Suppose our polynomial is

\[\begin{align} \epsilon x^2 - 2x + 1 = 0 \label{eq:seconddegree}\end{align}\]

and we say $\epsilon$ is a small number. Then we might guess the answer is of the form

\[\begin{equation} x = x_0 + \epsilon x_1 + \mathcal{O}(\epsilon ^2)\end{equation}\]

Let’s insert our guess in to our polynomial:

\[\begin{equation} \epsilon x^2 - 2x + 1 = \epsilon x_0^2 - 2(x_0 + \epsilon x_1)+1 = 0.\end{equation}\]

We’re neglecting all but first order terms. Remember that this must hold for arbitrary small $\epsilon$, so that we can divide this in to two equations, one involving the terms of zeroth order in $\epsilon$, and a first order equation. Like so:

\[\begin{equation} - 2x_0 + 1 + \epsilon (x_0^2 - 2x_1) = 0\\ \implies \begin{cases} - 2x_0 + 1 = 0\\ x_0^2 - 2x_1 = 0 \end{cases}\end{equation}\]

Well, sure enough, we can solve the first equation easily: the solution is $x_0 = \frac{1}{2}$. Inserting that in to the second equation, we get

\[\begin{equation} x_0^2 - 2x_1 = 0 \implies x_1 = \frac{1}{8}.\end{equation}\]

So the solution to our perturbation problem is $x = \frac{1}{2} + \frac{1}{8}\epsilon$. Easy!

But wait – what? Second degree polynomials have two roots, everyone knows that. What happened?

Well, we’ve all learned the formula for solving second degree polynomials, so let’s apply it. The exact solution of $\eqref{eq:seconddegree}$ is

\[\begin{equation} x_- = \frac{1-\sqrt{1-\epsilon}}{\epsilon}\\ x_+ = \frac{1+\sqrt{1-\epsilon}}{\epsilon}.\end{equation}\]

Well, why not apply perturbation theory to this form? Expanding around $\epsilon = 0$ using a Taylor series, we immediately get

\[\begin{equation} x_- = \frac{1}{2} + \frac{1}{8}\epsilon + \mathcal{O}(\epsilon ^2)\\ x_+ = \frac{2}{\epsilon } - \frac{1}{2} + O(\epsilon ).\end{equation}\]

Oh boy – as we set $\epsilon \rightarrow 0$, the second term solution goes towards infinity. Curse these second degree polynomials; they’re nonsense anyway; there’s no way this is rigorous; I should’ve studied art history..

The reader might be feeling quite betrayed. Have we really been beaten by a second degree polynomial of all things? Can’t a fella even trust elementary school algebra these days? Surely, when we know the answer ahead of time, we must somehow be able to get a sense of it perturbatively!

We can. You see, the choice of equation $\eqref{eq:seconddegree}$ is not really unique, is it? We could multiply it on both sides by some number, and it would still be zero. We could then do the reverse operation at the end to get the roots in terms of our original variable $x$.

This helps us, because our problem clearly arises from the fact that we’re treating the highest order part of the polynomial perturbatively. Since removing that term reduces the number of roots by one, we can’t possibly find the second root by applying perturbation theory naively. We have to get rid of the $\epsilon$ in front of $x^2$ and move it to some other term by scaling $x$. In other words, we have to renormalize. Indeed, define a new variable $w = \epsilon x$. Then $\eqref{eq:seconddegree}$ is

\[\begin{align} &\epsilon x^2 - 2x + 1 \rightarrow \frac{1}{\epsilon ^2}w^2 - 2 \frac{w}{\epsilon} +1=0 \\ & \iff w^2 - 2\epsilon w + \epsilon ^2 = 0\end{align}\]

Behold – all of our problems have disappeared. This form amenable to a perturbation treatment. You can solve this using the perturbation procedure outlined above and get a perfectly finite answer, and all we did is rescale the problem, just as you do in renormalizing QFT.

In some sense, the original variable $x$ just wasn’t good for what we were looking to do. We couldn’t recover two roots for a second order polynomial using that variable.

Of course, this problem is quite general with polynomial equations. Without changing variables, you’ll always get fewer roots than you should, and in fact the roots invisible to you are going to be sensitive to the perturbation parameter. Look at this polynomial:

\[\begin{equation} \epsilon x^6 + x^2 - 2x + 1 = 0 \label{eq:sixth}\end{equation}\]

The absolute values of as a function of $\epsilon$:

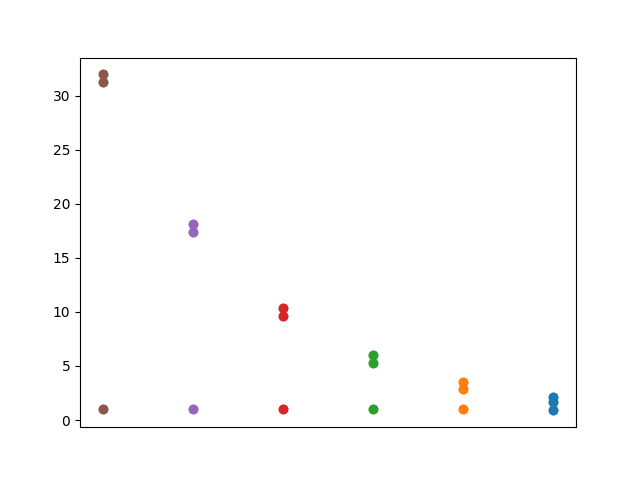
Notice how some of the values are highly sensitive to $\epsilon$, and they escape towards infinity as epsilon gets smaller (you can only see three, because they’re complex and have similar absolute values). Those are the values you wouldn’t find with perturbation theory.

Alright, you say, maybe this renormalization business isn’t so bad after all. I can now sleep my nights well and live without the constant anxiety caused by lurking infinities.

Hah, we’ve barely gotten started. If you thought our problems with quantum field theory end with the singularities of polynomials, then I have bad news for you. Here’s another serving of despair.

I got 99 problems

You see, just because you have managed to produce some finite terms in your little perturbation series, that doesn’t mean that the sum of those finite terms is in fact finite. Hell, look at this:

\[\begin{equation} S = \sum _{n=0}^\infty 2^n\end{equation}\]

Doesn’t look very finite, does it? So how do you know your series gives finite results?

To illustrate some divergent series, let’s take a nice normal function, not this crazy path integral business. Behold our guinea pig:

\[\begin{equation} Z = \int dxe^{-x^2 - \lambda x^4} \label{eq:normal}\end{equation}\]

Those familiar with QFT will note the suggestive name and form of this integral! Now evidently, if we have no "interaction" (the $x^4$ term), we get the result:

\[\begin{equation} Z = \sqrt{\pi}\end{equation}\]

The full solution to $\eqref{eq:normal}$ is

\[\begin{equation} \int e^{-x^2 - \lambda x^4}dx = \frac{e^{\frac{1}{8\lambda}}K_{1/4}\bigg(\frac{1}{8\lambda}\bigg)}{2\lambda} \label{eq:finite}\end{equation}\]

where $K$ is the modified Bessel function of the second kind – though it is not really important for our purposes here. The point is, in this case, we can solve the problem even without a "perturbation series". But anyway, let us proceed as we would in field theory, where we want to treat the $\phi ^4$ term perturbatively. First

\[\begin{align} \int d^4x e^{-x^2 - \lambda x^4} &= \int d^4x e^{-x^2}e^{-\lambda x^4} \\ &= \sum _{n=0}^\infty \int d^4x e^{-x^2} \frac{(-\lambda x^4)^n}{n!}\end{align}\]

Easy peasy. After some integrations and algebra, we get

\[\begin{equation} Z = \sum _{n=0}^\infty \sqrt{\pi}\frac{(-\lambda)^n(4n)!}{2^{4n}(2n)!n!} \label{eq:seriesexp}\end{equation}\]

Check with your favorite tool – this series is divergent.

Hold on! We started with a perfectly finite integral $\eqref{eq:finite}$, and ended up with an infinite series? Mumble mumble art history..

Here’s a question for you: when are you allowed to exchange the order of series and integral? Hint: not in this case. So we’ve created our problems by illegally changing the order of those two operations. Frankly, I’m shocked that a SWAT team has not bursted through my door as I write this – that’s how bad our math is. With finite intervals and finite sums, interchanging them is pretty much always allowed; but in the case of series and improper integrals, we have to be more careful than this.

The series in $\eqref{eq:seriesexp}$ is not hopeless, though. Here’s a funny plot:

The red line is the correct answer calculated with the Bessel function. So you see, as long as you cut off the series before it gets wild, you will get a useful approximation. Essentially, we will get punished for our lack of mathematical rigor after some number of terms in the series, but not immediately; the first few terms give increasingly accurate approximations for our integral.

In fact, we can give an estimation as to when the series will start to diverge, but I won’t do so here for a simple reason: the estimate for quantum electrodynamics is about $\mathcal{O}(100)$. That means we could calculate dozens of terms in the series before running in to any trouble with divergences. However, only the first 5 or 6 orders have been calculated, and it’s unlikely we’ll ever get much further than that, since the number of Feynman diagrams in each term of the series keeps increasing very rapidly. It’s also not particularly useful to calculate more terms given the limits of current experiments – why calculate more terms than experimental accuracy allows for?

The point with regard to QFT is this: in forming a perturbation series in the (path integral) quantum field theory, we actually do a similar swap between integral and sum (see next section). That is why the series in QFT is divergent.

I have now battered you with two types of infinities – infinities in individual expressions and infinities in series summation – and solved them easily (hey, just like, cut off your series man!). What does this have to do with QFT exactly? Well, I’ve already given you some hints. The following section contains some detail that you can skip if you don’t care.

What About QFT?

The main point of this text is that the infinities in QFT are not insurmountable, and that the problems discussed previously are in some sense analogous to problems in QFT. If you don’t care about QFT details, then you can skip this section.

Here’s how you do quantum field theory in the path integral formalism (which we use because it most conveniently illustrates the problem, though it also applies to the other formalisms). To get the propagator, you sum over all the fields like so:

\[\begin{align} \langle 0 | T \phi (x) \phi (x') |0\rangle &= \int D\phi \phi (x) \phi (x')e^{-\int d^4x \mathcal{L}} \label{eq:measure} \\ \mathcal{L} &= \frac{1}{2}\phi (x)(\partial ^\mu \partial _\mu - m^2)\phi(x) - \lambda \phi ^4 + J(x)\phi (x)\end{align}\]

Intuitively, this means "integrate over all possible field configurations". So if you were to divide your space in to little squares, forming a grid, then this integral would be

\[\begin{equation} \int D \phi F[\phi] = \int d\phi _1 d\phi _2 ..d\phi _n F(\phi _1, \phi _2 ... \phi _n) \label{eq:fi}\end{equation}\]

with $\phi _i$ the value of the field at grid point $i$. In an intuitive sense, the integral in $\eqref{eq:measure}$ is the limit of $\eqref{eq:fi}$ as $n\rightarrow \infty$.

Let us also define

\[\begin{equation} Z[\phi] = \int D\phi e^{-\int d^4 x[ \mathcal{L} + J(x)\phi (x)]} \label{eq:Z}\end{equation}\]

Here, $\phi ^4$ is our interaction term and $J$ is an arbitrary source, such as some sort of magnetic field we wish to treat classically. Now it is easy to see that we can split this thing to two parts

\[\begin{align} \int &D\phi \phi (x) \phi (x') e^{-\int d^4x \mathcal{L}} \\ &= \int D\phi \phi (x) \phi (x')e^{-\int d^4x \frac{1}{2}\phi (x)(\partial ^\mu \partial _\mu - m^2)\phi(x)+J(x)\phi (x)}e^{-\int d^4x \lambda \phi ^4} \label{eq:propagator}\end{align}\]

Now, it is more obvious than obvious that we can write the last exponential term, which we have conveniently separated from the rest, as a series

\[\begin{equation} e^{-\lambda x^4}=\sum _{n=0}^\infty \frac{(-\lambda ^nx^{4n})}{n!}\end{equation}\]

By some tricks that I won’t go in to here, you can write

\[\begin{equation} \int D\phi e^{-\int d^4x \frac{1}{2}\phi (x)(\partial ^\mu \partial _\mu - m^2)\phi(x)+J(x)\phi (x)} = C e^{-\int d^4x J(x)G_F(x-y)J(y)}\end{equation}\]

Here $G_F$ is the Green’s function, just as you know from QFT (this result is valid even when there are prefactors in front of the exponential – sort of). $C$ is a constant that won’t concern us here.

We now note that, since

\[\begin{equation} e^{-\lambda x^4}=\sum _{n=0}^\infty \frac{(-\lambda x^{4})^n}{n!}\end{equation}\]

we can write this in terms of derivatives of $J$. You see, $\frac{\delta}{\delta J}e^{J\phi} = \phi e^{J\phi}$, so that

\[\begin{equation} \sum _{n=0}^\infty \frac{(-\lambda ^nx^{4n})}{n!} = \sum _n e^{\bigg( \frac{\delta}{\delta J(z)} \bigg)^{4n}}e^{Jx }\end{equation}\]

See how that works? Of course, the two $\phi$ - fields in front of the exponential in $\eqref{eq:propagator}$ can also be written as $\frac{\delta}{\delta J(x)}\frac{\delta}{\delta J(x’)}Z[\phi]$ (recall the definition of $Z$ from $\eqref{eq:Z}$). So putting this all together, the propagator is:

\[\begin{equation} \langle 0 |T \phi (x) \phi (x')|0\rangle = C\frac{\delta }{\delta J(x)}\frac{\delta }{\delta J(x')}\sum _{n=0}^\infty \frac{\lambda ^n \frac{\delta ^{4n}}{\delta J(z)^{4n}}}{n!}Z[\phi ]\end{equation}\]

Right? All we did is write a few terms with derivatives of $J$ and expand the interaction term $\lambda \phi ^4$ as a series. Easy! Only thing is.. this series diverges, even if you manage to renormalize.

What? Curse this quantum field.. well, by now, you catch my drift.

You see, we’ve made a bit of a blunder here. We’ve exchanged the sum from $n=0$ to $\infty$ with the integral in $Z[\phi]$. And we can’t do that in this instance – as we just saw with the exponential function!

Well then, you say, why even bother swapping the integral and the series? Just do the integral once and for all!

If you can do that, go ahead. I dare you. And when you’ve solved the full interacting theory like that, send me an email with the solution – I promise I totally won’t publish it without mentioning you and steal the Nobel.

The story with renormalization of individual terms of a series is the same. We use an inappropriate variable ("bare mass", "bare coupling constant", etc) to describe our theory and we get punished for it.

The Problems Never End

So, hopefully you’re convinced that infinities in themselves are no cause for panic. Still, quantum field theory is not without its problems. There are other mathematical issues in the formalism which have not been resolved. The best attempt at a rigorous QFT is the algebraic QFT framework – but nobody has even managed to formulate 4-dimensional interacting theories in it; renormalization in QFT is essentially an unsolved problem, if you want total mathematical rigor.

Nevertheless, I hope this has helped to alleviate some of your disgust about the infinities in QFT. The divergences, though technically formidable compared to polynomials and simple integrals of one variable, are not really that concerning. Just as in the case of polynomials and exponential functions, there are reasonable ways to deal with the infinities that don’t involve "sweeping them under the rug". This fact is simply obscured by the considerable technical difficulty in doing field theory calculations.

For practical purposes, QFT is just fine.

Acknowledgement

The series material is lifted from "How I Learned To Stop Worrying and Love QFT" by R. C. Helling. The first polynomial perturbation example is standard, found for example in "A First Look at Perturbation Theory" by Simmonds and Mann. I can’t take credit for most of the ideas; I combined aspects of both of these sources with a bit of my own stuff added in to hopefully assist students struggling in QFT courses.