Baby's First Philosophy of Quantum Field Theory Article
On mobile devices, read the page in horizontal/"landscape" mode. Otherwise math may not fit the screen.If you’re even remotely interested in the philosophy of physics, you’ve surely heard of quantum mechanics. Hell, nowadays quantum mechanics is even in your washing machine – who among us would use non-quantum soap?1 No doubt you’ve heard all sorts of wonderful things about quantum particles instantly knowing what happens to their entangled partner, or being in two places at once, and so on.
Most of the things philosophers have talked about are essentially features of non-relativistic quantum mechanics; that is, the quantum mechanics of particles moving fairly slowly compared to the speed of light. Low-energy stuff. That’s understandable for two reasons. Firstly, most of the philosophically interesting features of quantum mechanics are already present in the non-relativistic version (and don’t by any means disappear in the relativistic version), so there’s plenty to discuss. Second, a lot of stuff in the real world is mostly dependent on these low-energy phenomena, such as the properties of materials, semiconductors and so on.
Nevertheless, there are legitimate reasons to (philosophically, morally, aesthetically, drunkenly) care about relativistic quantum mechanics – quantum field theory (QFT). Plenty of ordinary phenomena are not low-energy. For example, the sky is blue because of Rayleigh scattering, which is a relativistic phenomenon. So you need QFT – and it turns out that QFT not only inherits the normal quantum problems but adds new ones on top. This is an introduction to those issues.
I’ve written this article centering around two philosophers of QFT, Doreen Fraser and David Wallace. They take opposing viewpoints on important issues in the philosophy of QFT. I’ll admit my bias upfront – I think Wallace is right, Fraser wrong. I’ll try to give it a fair shake anyway, and regardless, this text is mostly intended as an introduction to the issues, not the particular argument.
Basic Argument
I will start by outlining the arguments in the papers in very general terms, skipping over details and technicalities. This has the advantage of immediately naming a host of important issues in QFT, which I’ll then deal with in turn in later sections.
Quantum field theory is more of a mathematical framework than a particular theory. The issue at hand is which version of QFT to use for foundational discussions about philosophy. Fraser believes we should use a QFT called "algebraic quantum field theory" (AQFT), a mathematically sophisticated version, whereas Wallace advocates for using "conventional quantum field theory" (CQFT), the theory practicing physicists actually do practical calculations in. Below, I’ve emphasized the words that I will explain in later sections.
Fraseer’s argument against using CQFT runs basically as follows. CQFT, as a theory, is mathematically ill-defined. If we use it in a naive fashion, the calculations end up giving infinite answers and running in to Haag’s theorem which basically proves the theory is inconsistent. We can only cure the infinities and avoid Haag’s theorem in a dubious fashion (renormalization), which causes the theory to lose its Lorentz-invariance. A theory this poorly defined can’t be suited to foundational work; rather, we should use AQFT, which has a mathematically sound definition and in which none of the above issues apply. And, after all, though AQFT is less-developed than CQFT, we already have examples of AQFTs in 2-dimensional spacetimes, and they’re equivalent to the same theory given in the CQFT formalism, so we should use the mathematically well-defined theory instead of an ill-defined mess. We have a genuine case of underdetermination of theory by evidence and must choose the foundationally sound theory.
Wallace’s counter-argument points out that while 2-dimensional examples of AQFT exist, there exist no 4-dimensional interacting AQFTs. And, as you may have noticed, we live in a 4-dimensional world (three spatial dimensions and time). Therefore, it’s not currently possible to construct the Standard Model of particle physics in the AQFT framework. You can, on the other hand, construct the Standard Model in CQFT just fine. Why would you use AQFT for foundational work when it can’t even construct the most succesful scientific theory we have? We should instead prefer CQFT, which is capable of the Standard Model. Wallace argues also that while renormalization may have been a dubious procedure in the 1950s, it is now a mathematically well-understood; any problems it causes with Lorentz-invariance have been made basically irrelevant by progress in renormalization theory.
Well, that was a mouthful, wasn’t it? Unless you’re already familiar with QFT, you probably didn’t understand most of it. Let’s fix that.
Unitary Inequivalence and Haag’s Theorem
Haag’s theorem is a brilliant result that demonstrates the inconsistency of quantum field theory – it basically shows the whole theory (in its CQFT formulation) is mathematically incoherent if applied naively. Here’s how it works.
Haag wrote down a bunch of obvious-looking assumptions about QFT. For example, he assumed it’s possible to uniquely define a state with no particles (duh - obviously you know what "no particles" means), and that the theory is Lorentz-invariant, that is to say, it obeys Einstein’s special relativity (speed of light is the maximum speed). All of the assumptions he made were a standard part of QFT. He then rug-pulled his audience by showing that they lead to a contradiction – you can’t possibly satisfy all the assumptions at the same time.
The bottom line is that trying to construct an interacting theory in this fashion means it’s not unitarily equivalent to the free theory. Unitarily equivalence basically (skipping over a fair few details) means that two theories can be described in the same mathematical context – that they’re, in a vague sense, physically equivalent. Don’t take this too seriously – the main point is unitarily equivalent = good, unitarily inequivalent = bad. In non-relativistic quantum mechanics, it turns out that any way to write down a proper quantum theory is unitarily equivalent to all the other ways, even if it looks different at first sight. In relativistic QFT, no such luck.
So basically, Haag’s theorem says QFT doesn’t work. This is one of the points Fraser makes in her article – how could we trust such a theory for foundational work? Unless..
Underdetermination
Underdetermination of theory by evidence – "underdetermination" for short – can basically (simplifying a bit again) mean two situations:
-
Two theories work just as well given all available evidence. Both theories explain the evidence that has been gathered.
-
Two theories work just as well given not only all available evidence, but even all evidence that could possibly be gathered. Any empirical predictions from the two theories will always agree.
The first variant is very common; it frequently happens that there isn’t enough evidence yet to favor one theory over another, but often later evidence appears to rule one of the theories out.
The latter case is more interesting and that is what Fraser has in mind in her paper: the predictions of AQFT and CQFT actually do agree to any given accuracy no matter what where AQFT exists.
The problem in the context of the article is that AQFT doesn’t exist for four spacetime dimensions, so we can’t really say there is any underdetermination there. In two dimensions, AQFT and CQFT are underdetermined, though, and one could reasonably argue that AQFT is a preferable theory.
Renormalization and the Renormalization Group
When physicists first started computing physical quantities with QFT, they ran in to an annoying issue: every result was infinite. Various people then invented ad-hoc methods to get around this infinity – they basically swept it under the rug by various tricks that were justified only in a haphazard intuitive fashion. This trickery was called renormalization, presumably because they feared calling it "bullshit" would have hindered the acceptance of the theory.
You can do this in a few ways, and it’s not obvious any of them really offer satisfactory physical reasons for renormalization. The basic idea is that you cut off certain properties to cure the infinities. A straightforward way to do this is to suppose that space is not continuous and smooth, but rather consists of blocks. These might be very tiny blocks indeed – far beyond the ability of human eyes or even particle accelerators to detect – but blocks nonetheless. This removes the infinities, and if you’re clever you can make the space smooth again while keeping the infinities away. This involves changing, for example, the physical mass of the particles in the theory to counterbalance the infinity. It turns out that doing so also escapes Haag’s theorem, since the procedure violates the assumptions going in to it.
Well, why not do that then? Because it doesn’t look like our space is in fact made of tiny blocks! True, the blocks might be invisible to us because we don’t have sophisticated enough equipment to see them, but the fact remains that we have no evidence for that. For practical reasons, physicists nevertheless use this trick, because even if it is foundationally unsatisfactory, it leads to correct experimental results.
There is another twist to this story, however. The procedure, it turns out, is not quite as "imaginative" as it seems – and Wallace uses this in his defence of the ordinary physicist, who goes on happily renormalizing.
In the 1970s, a brilliant fellow by the name of Ken Wilson was working on critical phenomena – physics of critical points, like when water turns to vapor or freezes to ice. Phase transitions!
He was working on a particular problem, which had to do with a block of pure metal with slight impurities of other materials sprinkled in. He realized that critical points were caused by phenomena at several scales working simultaneously. Typically, when investigating a matter theoretically, you assume one scale is relevant – either a high-energy or a low-energy situation; long length scales or short length scales, and so on. Wilson realized that critical points were so hard to understand because they involved multiple scales, and you couldn’t ignore any of them.
Wilson didn’t just think that, though. He developed a theory of how quantities change in different scales. He realized that phase transitions generally happen in points where calculations at all scales happen to agree.
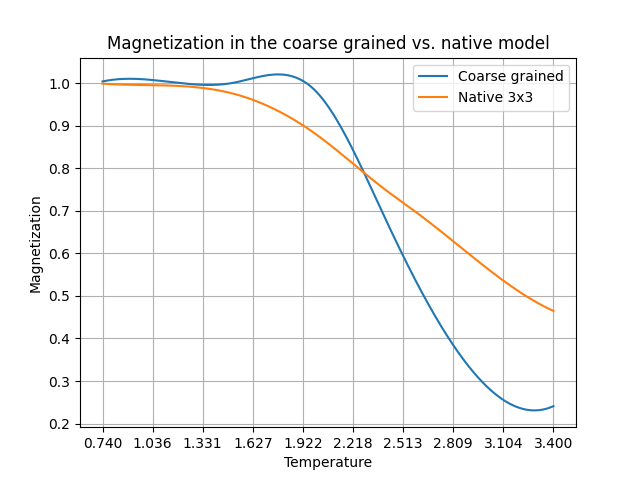
The basic way you do this type of calculation is as follows. You first calculate at one scale. Then you calculate it in a more fine-grained fashion – for example, if you had a 3x3 = 9 blocks of spacetime, you increase that to 9x9 = 81. Then you see what this finer calculation looks like in the coarse-grained case – you divide the 9x9 grid to 3x3 grids and calculate your quantity by averaging over those big blocks. So at the end, you have two results for the very same quantity.
In the image, I’ve done this calculation for the magnetization of a famous physics model (the Ising model) for magnetization in different temperatures. Notice where the two lines cross each other? That’s where the critical point is! That’s where both scales agree, and the Ising model loses its magnetization (that generally happens to magnets – if you heat them too much, they become non-magnetic).
So what does this have to do with renormalization? Well, Wilson showed that renormalization in QFT basically is this process! The way you choose the counter-terms to remove the infinities basically involves writing them as a function of the scale, and the way you can solve the dependence of e.g. physical mass on the scale is using Wilson’s renormalization group equations. Didn’t I tell you the guy was brilliant?
Wilson made sense of renormalization and discovered a deep connection between particle physics and solid matter physics. Soon after, he discovered a Nobel prize medal around his neck. Today, this method is used in various fields of physics (well – people have developed much more sophisticated algorithms, but the same basic principle).
What this has to do with our discussion is a bit more subtle. Basically, Wallace says that Wilson’s work on renormalization makes it completely reasonable to expect that if there’s a further theory – something deeper than QFT – then of course QFT is going to have oddities in it. That’s just a matter of scaling, like in the renormalization group equations. We don’t know what the theory beyond QFT is, but it is not unreasonable to expect it shows up as infinities in our current theory.
For example, imagine we wanted to model the surface of a metal. Instead of dealing with individual atoms, of which there are too many to handle, we might instead describe the surface as a field (this is a method actually used by condensed matter physicists!). Now if we try to calculate something at distances smaller than the distance between atoms on the surface, obviously we’re going to get some sort of nonsensical result – we’re modeling a bunch of atoms as a field, and if we try to go in between them, we get nonsense, because we’ve replaced the granular atomic surface with a continuous one by force. The small distances are meaningless in our model. They’re beyond the range of application.
Similarly, QFT probably has a scale at which it no longer makes sense. And that’s fine – Wilson’s renormalization group work tells us what to do with the scales we can access, and that the scales we can’t access show up in the theory in the renormalization group equations only indirectly. There’s no reason to panic if an infinity crops up when we try to go beyond it.
Bringing It Together
So, where does that leave us? AQFT is mathematically rigorous, but doesn’t exist in 4 dimensions. It offers a different view of the world from CQFT, which is mathematically sloppy but has the virtue of existing.
What is the difference? Well, for example, AQFT doesn’t really have quanta, which are basically particles. It does have something approximately like that, but it’s not a fundamental part of it like it is in CQFT.
Fraser also points out that if there’s really a fundamental theory beyond QFT, then we can expect there to be some conceptual continuity between that theory and QFT. That is, we should expect they rely on similar concepts. So if we’re relying on ill-defined concepts of CQFT, then might stray in our search for the elusive more fundamental theory – we’re trying to base it on the wrong concepts!
Wallace wants to say that QFT is approximately true and thus offers us an approximate guide to foundational philosophical work. Fraser wants to answer the question: if QFT were rigorously defined and exactly true, what does it say about the world?
I think Fraser’s problem is that her proposed theory doesn’t exist. This is a massive problem – if I started hitting on ladies by bragging about my imaginary Ferrari, I would quickly encounter a problem. Even if we conceded that CQFT is hopelessly bad as a theory (which it clearly isn’t, since it is at least empirically succesful!), that would give us no reason whatsoever to trust what AQFT says about short-distance physics. Until a realistic AQFT theory exists – one that is capable of reproducing the Standard Model – it seems foolish to trust anything it says about physics.
In any case, hopefully you learned something about the phraseology of this field of philosophy. The articles I based this on are Wallace’s "Taking particle physics seriously: A critique of the algebraic approach to quantum field theory" (2011) and Fraser’s "Quantum Field Theory: Underdetermination, Inconsistency, and Idealization" (2009).