Variational Calculus in Your Face

On mobile devices, read the page in horizontal/"landscape" mode. Otherwise math may not fit the screen.

One of the great shocks in the undergraduate’s life is the introduction of variational calculus. Many a student has fled the physics department in horror, never to return; the couches of psychotherapists are filled with those unable to withstand the memory of deriving Euler-Lagrange equations.

I didn’t feel particularly comfortable with variational calculus when it was introduced to me. That problem probably originates in the way that variations were used: at least for my classes, they were used to get the Euler-Lagrange equations in the most common form, and then more or less forgotten about. That I didn’t understand all the steps in the derivation probably didn’t help.

Euler-Lagrange equations have a very special character: they require a functional of the form

\[\begin{aligned} S = \int dt L(t, x(t), \dot{x}(t)) \label{eq:action}\end{aligned}\]

which you then do a variation on to get the equations. This seemed weird to me at the time: sure, in classical physics the Lagrangian was generally of that form, but is this all variational calculus is good for? It’s like talking about derivatives exclusively by introducting the derivative of $y=x^n$.

In general, variational calculus deals with functionals – maps from a space of functions to numbers. The action, for example, takes the path of a particle $x(t)$ and spits out a number (the action).

The Euler-Lagrange equations say the following: the correct physical path of a particle is the one that minimizes the action. Recall that when we want to find the maximum or minimum of a function, we calculate its derivative and seek the zeroes. The same is true in variational calculus: we calculate the "functional derivative" and find its zeroes. That’s what we will now try to construct.

Why should I care in the first place?

A historical digression is in order. The classical problem in the calculus of variations is the so-called brachistochrone problem. Given a point A and a lower point B, suppose a slide of some kind connects them. If we want to roll a ball down this slide as quickly as possible (assuming only gravity acts on it), what shape should the slide be?

Johann Bernoulli presented this problem with much pomp and circumstance:

I, Johann Bernoulli, address the most brilliant mathematicians in the world. Nothing is more attractive to intelligent people than an honest, challenging problem, whose possible solution will bestow fame and remain as a lasting monument. Following the example set by Pascal, Fermat, etc., I hope to gain the gratitude of the whole scientific community by placing before the finest mathematicians of our time a problem which will test their methods and the strength of their intellect. If someone communicates to me the solution of the proposed problem, I shall publicly declare him worthy of praise. ¹

Newton solved the problem easily, of course. However, he sent his solution in anonymously because he didn’t "love to be dunned [pestered,bothered] and teased by foreigners about mathematical things..." His attempted anonymity was no help at all, because Bernoulli immediately "recognized the lion by his claw".

Well, what is the problem in modern notation? First, what is the speed of the ball after dropping a height $y$? Well, according to conservation of energy, the potential energy transforms in to kinetic energy: \(\begin{aligned} \frac{1}{2}mv^2=mgy \implies v=\sqrt{2gy}. \end{aligned}\)

When a the moves an infinitesimal distance $ds$ in some direction, we break down the change to a small change in the x direction – $dx$ – and a corresponding small change to the y direction. Then by the Pythagorean therem $ds^2 = dx^2+dy^2$ in terms of infinitesimals. And

\[\begin{aligned} dx^2+dy^2 &= \bigg[\bigg(\frac{dx}{dx}\bigg)^2+\bigg(\frac{dy}{dx}\bigg)^2 \bigg](dx)^2\\ &= (1 + y'(x)^2)(dx)^2. \end{aligned}\]

I’ve used ‘ to indicate derivative with respect to x. Then, since time is $t = s/v$ with s the distance, and our path is a sum of little bits of s ($ds$ – remember that integrals are basically sums!), we integrate from point A to point B:

\[\begin{aligned} t &= \int _{\gamma} \frac{ds}{v} \\ &= \int_{A_x}^{B_x}\frac{\sqrt{1+y'(x)^2}}{\sqrt{2gy(x)}}dx. \end{aligned}\]

The problem is to find the curve $y(x)$ that minimizes this time. The procedure to do so, as we will find out, is much like trying to find the minimum of a function by calculating its derivative. Not an immediately easy problem to solve! Bernoulli himself took two weeks. This is of course just a taste – there are many, many problems in physics that are usually solved by variational calculus. It’s just a particularly elegant problem, and as Huygens said, we should not be content to amuse ourselves by analyzing problems "made up solely for using geometrical calculus upon them"².

What’s a variation?

To reiterate, variation is sort of like "the derivative of functionals". To solve a problem of minimizing a functional, we typically want to find the zero of this derivative.

For functions like $y=x^2$, the derivative at point $x_0$ is the "slope" of the function at that point; it tells us how much the function changes if you change $x$ a little bit. Informally, you could calculate it by doing

\[\begin{aligned} y+dy = (x+dx)^2 &= x^2+2xdx+(dx)^2 \approx x^2+2x dx \\ &\implies dy/dx = 2x. \end{aligned}\]

where the idea is that since $dx$ is small, $dx^2$ is so small as to not matter. The concept is the same for variations ("functional derivatives"), except that now the points in space are functions. So, when we talk about the "functional derivative" at point $x_0$, that point is actually a function in a space of functions.

So, how do we move "a little bit" in function space? Well, variations are defined on some interval, and the variation shouldn’t change the value of the function at the limits of the integral (beginning and end of the path) for reasons that will become obvious soon. For example, let’s say our interval is $[-2,2]$ and we’re in the space of functions that have a finite integral on it. For example, the function $y(t)=t^2$ has a finite integral on $[-2,2]$. One example of a variation would be

\[\begin{aligned} &y(t) + \epsilon \eta (t) \\ &= t^2 + \epsilon \sin \bigg(\frac{\pi}{2}t\bigg). \end{aligned}\]

Clearly, $\eta (t)$ vanishes at $-2$ and $2$ (check for yourself if you don’t believe me). Here’s a picture of the situation:

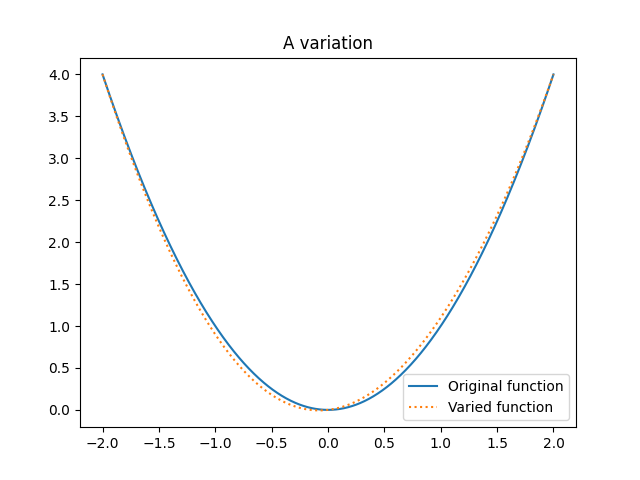
This is not the only variation you could come up with, in stark contrast to derivatives where there’s really only one way to "move a little bit". In fact, you should try to think of another one! The key idea is that we don’t restrict these variations too much – we just say they must vanish at the limits of our interval and possess some nice regularity properties. The usual suspects – derivatives exist, blah blah blah; if you pick a bad variation, you’ll certainly notice when things blow up.

Functional derivatives

Let’s take a simple functional:

\[\begin{aligned} F = \int _{-2}^2 y(t)^2 dt . \end{aligned}\]

Just as in the case of normal derivatives we want to see what happens to the function when you change the argument a little bit, we now want to see what happens to the functional when we change the function a little bit. So let’s change $y(t)$ a little bit by $\epsilon \eta (t)$:

\[\begin{aligned} F[y(t) + &\epsilon \eta (t)] - F[y(t)] \\ &= \int _{-2}^2 \bigg[(y(t)+\epsilon \eta (t))^2-y(t)^2\bigg]dt\\ &=\int _{-2}^2 \bigg[y(t)^2 + 2\epsilon \eta (t) y(t) + \epsilon ^2 \eta (t)^2 - y(t)^2\bigg]dt\\ &=\int _{-2}^2 \bigg[2\epsilon \eta (t) y(t) + \epsilon ^2 \eta (t)^2 \bigg]dt \end{aligned}\]

Since $\epsilon$ is supposed to be a small number, we can say that $\epsilon^2 \approx 0$. So we have:

\[\begin{aligned} \int _{-2}^2 \bigg[2\epsilon \eta (t) y(t) + \epsilon ^2 \eta (t)^2 \bigg]dt \approx \int _{-2}^2 \bigg[2\epsilon \eta (t) y(t)\bigg]dt. \end{aligned}\]

$\epsilon \eta (t)$ is arbitrary. Thus, if we wanted to minimize this variation by setting it to zero, we would require $2y(t)=0$. Otherwise the integral couldn’t be zero for arbitrary variations. That’s why we call $2y(t)$ the functional derivative. This idea can immediately be formalized: the functional derivative $\frac{\delta F}{\delta y}$ of functional $F$ is

\[\begin{aligned} \lim _{\epsilon \rightarrow 0} \frac{F[y(t) + \epsilon \eta (t)] -F[y(t)]}{\epsilon} = \int \frac{\delta F}{\delta y} \eta (t)dt. \end{aligned}\]

So, what we want to do is first calculate the difference $F[y+\epsilon \eta]-F[y]$, divide by $\epsilon$ and then set $\epsilon = 0$ and wrangle the expression in to the above form.

Let’s use an example from physics. The action for a free particle is

\[\begin{aligned} S=\int _{t_1}^{t_2} \frac{1}{2}m \dot{x}(t)^2 dt. \end{aligned}\]

From Newton, we know that the correct path for a free particle should be a straight line. No force, no acceleration, no change in velocity! Let’s see what we get:

\[\begin{aligned} &S[x(t)+\epsilon \eta (t)] - S[x(t)] \\ &= \int _{t_1}^{t^2} \frac{1}{2}m(\frac{d }{dt}x(t) + \epsilon \frac{d }{dt}\eta (t))^2 - \frac{1}{2}m \dot{x}(t)^2 dt\\ &= \int _{t_1}^{t^2} \frac{1}{2}m \dot{x}(t)^2 +\epsilon \frac{d}{dt}\eta (t) \frac{d }{dt}x(t) - \frac{1}{2}m \dot{x}(t)^2 + \epsilon ^2 \eta (t)^2dt.\\ &= \int _{t_1}^{t^2} m\epsilon \frac{d}{dt}\eta (t) \frac{d }{dt}x(t) + m\epsilon ^2 \eta (t)^2dt. \label{eq:resu1} \end{aligned}\]

Well, we have a problem. In our definition for the functional derivative, we had $\eta (t)$ as a common factor, like so:

\[\begin{aligned} \lim _{\epsilon\rightarrow 0}\frac{S[x(t)+\epsilon \eta (t)]-S[x(t)]}{\epsilon}=\int _{t_1}^{t_2} \frac{\delta S}{\delta x(t)} \eta (t) dt. \end{aligned}\]

Now, we have the derivative of $\eta$. We need to get rid of it.

Fortunately for us, we can use partial integration. Like so:

\[\begin{aligned} &\int _{t_1}^{t^2} \epsilon \frac{d}{dt}\eta (t) \frac{d }{dt}x(t) dt \\ &= \bigg[ m\epsilon \eta (t) \frac{d x(t)}{dt} \bigg]_{t_1}^{t_2} - \int _{t_1}^{t_2} m\frac{d^2 x(t)}{dt^2} \epsilon \eta (t) dt. \end{aligned}\]

You see now why we want the variation to vanish at the edges of our interval! If it didn’t, then the first term would not be zero and we would be left with a weird constant floating around. Who the hell needs that?

Remember what we must do next: divide by $\epsilon$ and set $\epsilon = 0$. Clearly, the term proportional to $\epsilon ^2$ vanishes and we’re left with

\[\begin{aligned} \lim _{\epsilon \rightarrow 0}\frac{S[x(t) + \epsilon \eta (t)]-S[x(t)]}{\epsilon}=\int _{t_1}^{t_2} -m\frac{d^2 x(t)}{dt^2}\eta (t)dt. \end{aligned}\]

Now by comparing with our earlier definition of a functional derivative, we see that

\[\begin{aligned} \frac{\delta S}{\delta x(t)} = -m\frac{d^2 x(t)}{dt^2}. \end{aligned}\]

If we want the functional derivative to be zero, then we get

\[\begin{aligned} \frac{\delta S}{\delta x(t)} = 0 \iff -m\frac{d^2 x(t)}{dt^2} = ma = 0. \end{aligned}\]

Notice that this is why we want to get the $\eta (t)$ as a common factor: because it’s arbitrary, we can discard it when requiring the functional derivative to be zero; it forces the other part of the integral to be zero since otherwise the integral couldn’t vanish for arbitrary $\eta (t)$.

But this equation is clearly just Newton’s equation of motion for zero force! And what we have done is minimized the Lagrangian with respect to particle path – in other words, we’ve implicitly used the Euler-Lagrange equations.

So we don’t need no stinking Euler-Lagrange equations. Just write down the action and do the variation until you’ve wrangled it in to the form $\int \delta S / \delta x \eta (t)dt$ and set the functional derivative to zero.

Let’s calculate another example – everyone’s favorite physics system, the beloved harmonic oscillator. The action is

\[\begin{aligned} S = \int _{t_1}^{t_2} \frac{1}{2}m\dot{x}(t)^2 - \frac{1}{2}kx(t)^2dt \end{aligned}\]

Now the first term is exactly the same as previously, so we know what the result of that is. All we need to do is calculate the variation of the force term.

\[\begin{aligned} &\lim _{\epsilon \rightarrow 0}\frac{S[x(t) + \epsilon \eta (t)]-S[x(t)]}{\epsilon} \nonumber\\ &= \int _{t_1}^{t_2}-\frac{d^2 x(t) }{dt^2} \eta (t)dt - \lim _{\epsilon \rightarrow 0}\frac{1}{\epsilon }\int _{t_1}^{t_2}\frac{1}{2}k(x(t)+\epsilon \eta (t))^2 - \frac{1}{2}k(x(t))^2 dt \nonumber\\ &= \int _{t_1}^{t_2}-\frac{d^2 x(t) }{dt^2}\eta (t)dt - \lim _{\epsilon \rightarrow 0}\frac{1}{\epsilon }\int _{t_1}^{t_2} kx(t) \epsilon \eta (t) dt \nonumber\\ &= \int _{t_1}^{t_2}-\frac{d^2 x(t) }{dt^2}\eta (t)dt - \int _{t_1}^{t_2} kx(t) \eta (t) dt \end{aligned}\]

We can identify the functional derivative again: it is

\[\begin{aligned} \frac{\delta S}{\delta \eta} = -m\frac{d^2 x(t) }{dt^2} - kx(t) \end{aligned}\]

and setting it to zero we get

\[\begin{aligned} m\frac{d^2 x(t) }{dt^2} = -kx(t) \end{aligned}\]

which is of course the correct spring equation.

To recap, here’s the algorithm to find the equations of motion for a system in physics from a Lagrangian:

1. Calculate $\lim _{\epsilon \rightarrow 0}\frac{S[x(t) + \epsilon \eta (t)]-S[x(t)]}{\epsilon}$.

2. Wrangle the expression you just calculated in to form $\int \frac{\delta S}{\delta x(t)} \eta (t) dt$. Partial integration should be applied to the derivatives.

3. Once you have identified $\delta S / \delta x(t)$, set it to zero. This is the equation of motion.

This procedure is general: it doesn’t require the action to be of a particular form. Let’s finish off by applying our procedure to the brachistochrone problem I introduced in the beginning.

Back to the brachistochrone

The functional in this case was

\[\begin{aligned} S = \int _{A_x}^{B_x} \frac{\sqrt{1+y'^2}dx}{\sqrt{2gy}}. \end{aligned}\]

I’m going to use $y’$ to denote derivatives with respect to x. You should understand $y$ to be a function of x. Then the variation:

\[\begin{aligned} &\lim _{\epsilon \rightarrow 0}\frac{S[x(t) + \epsilon \eta (t)]-S[x(t)]}{\epsilon} \\ &= \lim _{\epsilon \rightarrow 0}\frac{1}{\epsilon}\bigg[\int _{A_x}^{B_x} \frac{\sqrt{1+(y+\epsilon \eta )'^2}dx}{\sqrt{2g(y+\epsilon \eta )}} - \int _{A_x}^{B_x} \frac{\sqrt{1+y'(x)^2}dx}{\sqrt{2gy}} \bigg]. \end{aligned}\]

We can take the limit directly (there’s a challenge for you!), from which we get

\[\begin{aligned} &\lim _{\epsilon \rightarrow 0}\frac{S[x(t) + \epsilon \eta (t)]-S[x(t)]}{\epsilon}\\ &= \int _{A_x}^{B_x} \frac{g y(x) \eta '(x) y'(x) + g\eta (x) (-y'(x)^2-1)}{\sqrt{2}(gy(x))^{3/2}\sqrt{y'(x)^2+1}} \end{aligned}\]

The first term has the derivative of $\eta$, so we do a partial integration. After some manipulation:

\[\begin{aligned} &\lim _{\epsilon \rightarrow 0}\frac{S[x(t) + \epsilon \eta (t)]-S[x(t)]}{\epsilon} \\ &= \int _{A_x}^{B_x}-\frac{g(2y(x)y''(x)+y'(x)^2+1)}{2\sqrt{2}(gy(x))^{3/2}(y'(x)^2+1)^{3/2}}\eta (x) dx \end{aligned}\]

We can now identify the functional derivative and set it to zero. After simplifications we get

\[\begin{aligned} y''(x) = \frac{-y'(x) -1}{2y(x)}. \end{aligned}\]

The process here was not in principle more complicated than for the basic Lagrangians of classical mechanics. Only the algebraic manipulations are complicated; you can do the limits and rearranging of terms by using some software like Mathematica or SageMath.

I much prefer deriving my equations of motion this way, using the more general method that seems less arbitrary to me. Join me as a cool functional derivative enjoyer.

1. Bernoulli Acta Eruditorum, 18 : 269 (1696) ↩

2. https://www.dbnl.org/tekst/huyg003oeuv10_01/huyg003oeuv10_01_0039.php

   • transl. by

   https://intellectualmathematics.com/blog/learn-calculus-like-huygens/ ↩